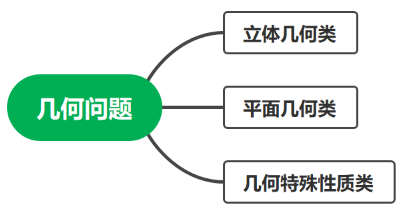
几何问题常考题型包含平面几何类、立体几何类与几何特殊性质类，因此我们从这三类常考题型给大家展开讲解。
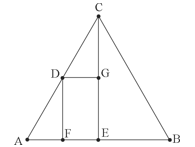
【例1】(单选题)某围场的形状为边长100米的等边三角形，在场地正中修建一座信号塔，塔顶安装有效覆盖半径为 
米的信号发射器。如要信号覆盖整个围场的地面，则信号塔的高度最高为多少米?
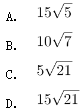
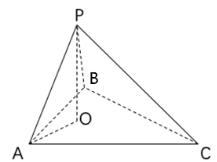
【解析】第一步，本题考查几何问题，属于立体几何类。
第二步，等边三角形重心、内心、外心、垂心重合于一点，此点称为等边三角形的中心。围场的正中心即等边三角形各边中线的交点。如图所示，根据一个角是30°的直角三角形的三边比例(1： 
：2)可知三个顶点每个顶点到中心O的距离都是
米。
第三步，信号塔最高点到最低点PO与OA、OB、OC都可以构成直角三角形。在直角三角形POA中，PA=
，OA= 
，根据勾股定理可知PO²=PA²-OA²=(
)²-(
)²=700，则PO=
(米)。
因此，选择B选项。
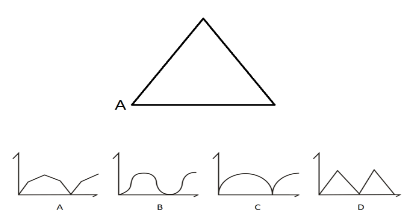
【例2】(单选题)一正三角形小路如下图所示，甲、乙两人同时从A点出发，朝不同方向沿小路散步，已知甲的速度是乙的2倍。问以下哪个坐标图能准确描述两人之间的直线距离与时间的关系(横轴为时间，纵轴为直线距离)( )
【解析】第一步，本题考查几何问题，属于平面几何类。
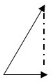
第二步，根据同时出发，且速度“是2倍”可以得到，在甲到达顶点之前的任意时刻，两人行走距离之间满足如图关系，斜边长是底边的2倍，可推出高度为底边的
倍，即距离和时间成线性比例关系，排除选项B、C。
第三步，讨论分界点，在“正三角形”中，当甲达到最高点时，乙到达底边中点位置，两者距离最大;当甲到达底边端点，两人相遇，距离最短为0。然后继续重复上述过程，故变化趋势只有两种状态，排除选项A。
因此，选择D选项。
【拓展】这个题目想考的就是你会不会选择临界点。同时在A出发两人之间距离为0.随着时间推移，当甲到达三角形的顶点时候，乙在顶点正对着那条边中点，两人距离是最长的。再随着时间推移，两人距离又慢慢减少直至为0，最后在三角形右下角的点汇合。如此重复循环。所以答案选D。这道题大家在考场上是可以在一分钟之内做出来的。
【例3】(单选题)一个人工湖的湖面上有一个露出水面3米的圆锥体人工景观(底面朝下)。如人工湖水深减少20%，则该景观露出水面部分的体积将增加61/64。问原来的人工湖水深为多少米?
A. 3.5
B. 3.75
C. 4.25
D. 4.5
【解析】第一步，本题考查几何问题，属于几何特殊性质类。
第二步，水深变化前后体积比为1：( 
)=64：125，那么圆锥前后的高度之比为4：5，原来是3米，则水深减少之后是3÷
=3.75米。前后水深减少了0.75米是人工湖水深的20%，那么人工湖水深为0.75÷20%=3.75米。
因此，选择B选项。
