第一种方法:箭头法
关键点:找一个特殊面画箭头,然后看画箭头面的上下左右的面是否发生改变,如果发生变化,便是错误选项,可直接排除。
下面我们用具体的例题来进行演示。
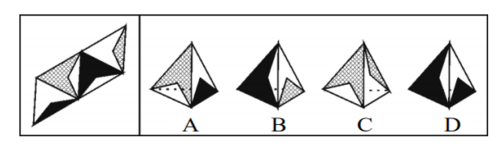
【例1】左边给定的是纸盒外表面的展开图,右边哪一项能由它折叠而成?
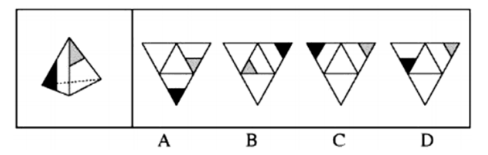
【解析】如下图所示,通过观察,发现四个选项都有①或②面,那么此时在题干中我们就可以先以①面为标准来画箭头,此时①面的左边应该为②面,如下图所示:
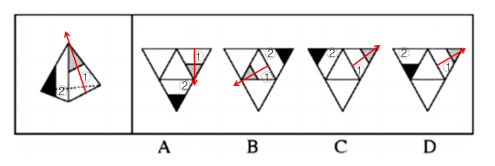
在上图的四个选项中,A项中的②面可以逆时针方向旋转180°,C、D项中的②面可以顺时针方向旋转180°,可发现此时三个选项中的②面都在①面箭头的左边,所以此时无法排除。但是B项中可发现②面在①面箭头的下边,所以位置关系发生改变,可直接排除。
此时,我们可以再以②面为标准来画箭头,那么②面的下边是①面,如下图所示:
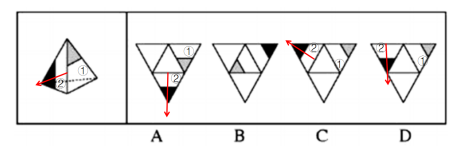
在上图中,A、C项中②面箭头的下边并不是①面,所以位置关系发生变化,可直接排除。因此,此题正确选项为D选项。
上述的箭头法基本可以解决一般性的题目,但是也存在一些弊端,即在一些题目中的某些选项不能适用此方法。所以,如果我们遇到这种情况时,那么我们可以运用下面的第二种方法来解决。
第二种方法:重合边法
关键点:看相邻面的重合边是否发生改变,如果发生变化,便是错误选项,可直接排除。如下例题:
【例2】左边给定的是纸盒外表面的展开图,右边哪一项能由它折叠而成?
【解析】通过观察,因为A、C项有相同的②面,所以可以在题干中及AC项中的②面画箭头,如下图所示:
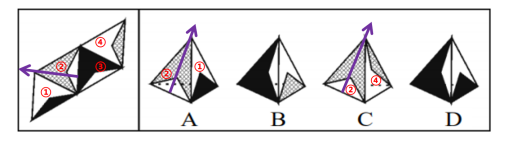
题干中的②面的箭头关系为,它的底面是③面,左边是①面,右边是④面(④面可逆时针方向旋转180°)。A项中②面右边是①面,而实际上①面应该在左边,所以位置关系发生变化,为错误选项,可排除;C项中②面右边是④面,与题干一致,暂时保留。
其次再来看B、D项,我们以③面画箭头,如下图所示:
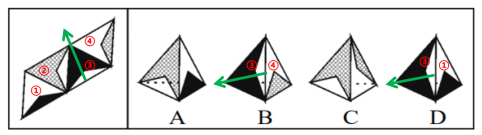
题干中的③面的箭头关系为,它的底面是①面(①面可逆时针方向旋转180°),左边是②面,右边是④面。B项中③面的底面是④面,而实际上④面应该在右边,所以位置关系发生变化,为错误选项,可排除;D项中③面的底面是①面,与题干一致,暂时保留。
通过上面的两种情况,仅仅看箭头的上下左右位置关系可发现C、D项的位置关系都正确。那么遇到这样的情景我们就可以第二种方法“重合边法”来解决,如下图所示:
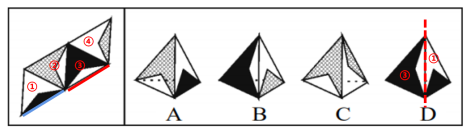
题干中①③面的重合边应该是“①面中的黑色黑色三角形的黑色底边与③面白色三角形的白色底边”相重合(即黑边与白边重合),但是D项中的①③面的重合边都是白色的边,所以重合边发生改变,为错误选项,可排除。因此,此题正确选项为C项。
所以,在我们实际的备考过程中,要想熟练运用这两种方法,平时一定要多用一些例题来练习,以巩固这两种方法。即在实际的题目中,如果用箭头法能直接排除选项就直接排除,不能直接排除的选项就要想到用重合边来解决。