在资料分析的材料中我们可以看到很多百分数,资料分析很多题目难就难在计算,有些资料分析计算量非常大,在解答与材料相关的题目时,基本上都会用到百分数。很多百分数都可以转化为特征的分数。如果在实际考试中能够把一些百分数转化为与之接近的特征分数,那将大大的简化运算,减少计算量。百分数的应用主要有三种:百化分、取整和插值。今天我将重点讲讲百分数应用之百化分。
一、常见特征数字的总结
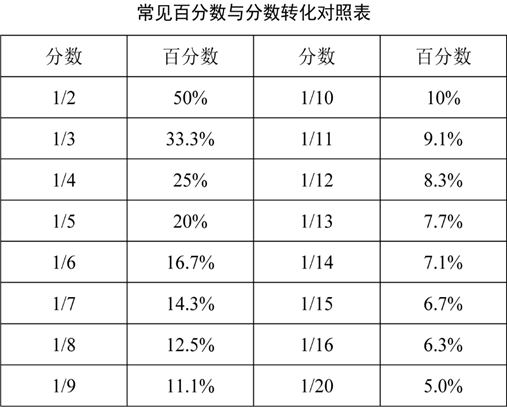
以上便是在资料分析中常用的一些特征的百分数和分数之间的转换。
二、百化分的具体应用
资料分析的题目计算中常常会出现百分数,对于这类题目,只要题目中有百分数,我们就可以尝试用百化分,不管是乘法还是除法运算,只要有百分数,并且可以找到对应的特征分数,就尝试用百化分。
【例1】4245×12.5%≈( )
A. 499 B. 531
C. 555 D. 583

解析:12.5%=![]() ,因此4245×12.5%=4245×
,因此4245×12.5%=4245×![]() =531
=531
【答案】B
【例3】610×51.4%×24.2%≈( )
A.66 B. 71
76 D. 82

解析:51.4%≈![]() ,24.2%≈
,24.2%≈![]() ,因此610×51.4%×24.2%≈610×
,因此610×51.4%×24.2%≈610×![]() ×
×![]() =76.25
=76.25
【答案】C
三、百化分的重点应用
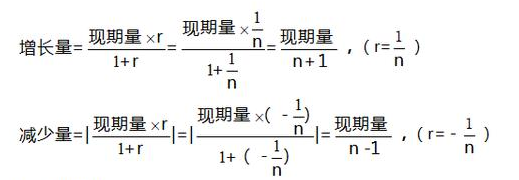
当题目中给定了现期量和增长率,我们可以用![]()
【例1】 2018年全年能源消费总量46.4亿吨标准煤,比上年增长3.3%。其中,煤炭消费量增长1.0%,原油消费量增长6.5%,天然气消费量增长17.7%,电力消费量增长8.5%。煤炭消费量占能源消费总量的59.0%,比上年下降1.4个百分点;天然气、水电、核电、风电等清洁能源消费量占能源消费总量的22.1%,上升1.3个百分点。
2018年,全上能源消费总量同比增长约多少亿吨标准煤?
A.0.9
B.1.5
C.2.1
D.2.5
【答案】B
【解析】
第一步,本题考查已知现期量与增长率的增长量计算问题。
第二步,定位文字材料“2018年全年能源消费总量46.4亿吨标准煤,比上年增长3.3%![]() ”。
”。
第三步,根据增长量=现期量×增长率/(1+增长率),3.3%≈,利用增长量计算n+1原则可得![]() 。
。
因此,选择B选项。
【例2】 2017年末全上农村贫困人口3046万人,比上年末减少1289万人,比2012年末减少6853万人;贫困发生率(指年末农村贫困人口占目标调查人口的比重)为3.1%,比2012年末下降7.1个百分点。2017年全上贫困地区农村居民人均可支配收入9377元,比上年增长10.5%。
2017年全上贫困地区农村居民人均可支配收入比上年增加的金额是:
A.782元
B.853元
C.891元
D.1069元
【答案】C
【解析】
第一步,本题考查已知现期量与增长率的增长量计算问题。
第二步,定位文段,“2017年全上贫困地区农村居民人均可支配收入9377元,比上年增长10.5%”。
第三步,根据增长量=现期量×增长率÷(1+增长率),10.5%![]() ,利用增长量计算n+1原则,得2017年全上贫困地区农村居民人均可支配收入比上年增加
,利用增长量计算n+1原则,得2017年全上贫困地区农村居民人均可支配收入比上年增加![]() 元,直除首两位商89。
元,直除首两位商89。
因此,选择C选项。
【本题结束】
【例3】 2015年全上共建立社会捐助工作站、点和慈善超市3.0万个,比上一年减少0.2万个,其中:慈善超市9654个,同比下降5.1%。全年共接收社会捐赠款654.5亿元,其中:民政部门接收社会各界捐款44.2亿元,各类社会组织接收捐款610.3亿元。
2015年,全上建立的慈善超市较2014年约:
A.减少519个
B.增加519个
C.减少686个
D.增加686个
【答案】A
【解析】
第一步,本题考查已知现期量与增长率的增长量计算问题。
第二步,定位文字材料“2015年慈善超市9654个,同比下降5.1%”。
第三步,由于同比下降,优先排除BD选项。根据减少量=(现期量×减少率)/(1-减少率),![]() ,利用减少量计算n-1原则可得
,利用减少量计算n-1原则可得![]() ,直除首位商5。
,直除首位商5。
因此,选择A选项。










