【例1】已知三角形三边长分别为3、15、x。若x为正整数,则这样三角形有多少个?
A. 3个 B. 4个
C. 5个 D. 无数个
【答案】C

【解析】本题考查几何特性,三角形三边关系。![]() ,即
,即![]() ,所以x可以为13、14、15、16、17,共5个。故本题选C。
,所以x可以为13、14、15、16、17,共5个。故本题选C。
此题选项数据比较小可以直接枚举为5个,若数据较大则直接让两个数相减再减一即![]() (个),边端计数注意点和间隔数的区别,两端均不可取则间隔数减一。
(个),边端计数注意点和间隔数的区别,两端均不可取则间隔数减一。
本题是直接考查三角形三边关系,比较简单。近几年上、联考对三角形三边关系的考查侧重于第二种题型,间接考查。
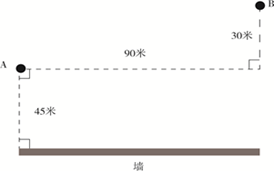
【例2】(2019年浙江)A点、B点与墙的位置如右图所示,现从A点出发以5米/秒的速度跑向墙,接触到墙后再跑到B点,问最少要多少秒到达B点?

A.30 B.34
C.38 D.42
【答案】A
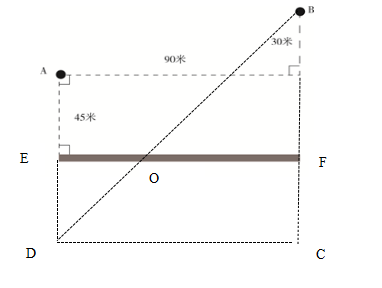
【解析】本题结合行程间接考查几何特性。找A点关于墙的对称点D,连接BD,与墙交于O点,则O点即为到两点之和最短的点。过B点作墙的垂线BF并延长,与过D点墙的平行线,交于C点,则三角形BCD为直角三角形。DC=90(米),BC=30+45+45=120(米),根据勾股定理,3:4:5的关系易知![]() (米)。所需最短时间为
(米)。所需最短时间为![]() (秒)。故本题选A。
(秒)。故本题选A。

本题虽然虽然需要做辅助线,但属于平面的几何构造,只要知道这一特性还是很容易求解的,在2021年联考考查这一特性则结合立体图形一起考,难度加大。
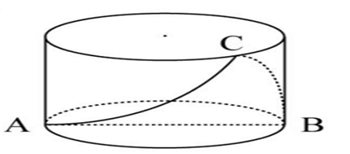
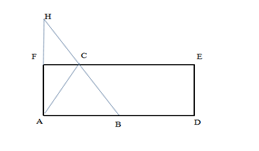
【例3】一个不计厚度的圆柱型无盖透明塑料桶,桶高2.5分米,底面周长为24分米,AB为底面直径。在塑料桶内壁桶底的B处有一只蚊子,此时,一只壁虎正好在塑料桶外壁的A处,则壁虎从外壁A处爬到内壁B处吃到蚊子所爬过的最短路径长约为:

A.10.00分米 B.12.25分米
C.12.64分米 D.13.00分米
【答案】C
【解析】本题考查几何问题,几何构造。从外壁最终到内壁,最短情况有可以是:
第一种:从A点沿着外壁竖直上去再竖直下来,接着径直从A点爬到B点,走过的总长为![]() (分米)。
(分米)。

第二种:将圆柱展开成平面,为一矩形ADEF,AB长度为圆周的一半12分米,作A点关于直线EF的对称点H,连接AC+BC=BH,即为壁虎吃到蚊子所爬行的最短距离,根据勾股定理可知![]() =(分米)。
=(分米)。
所以最短距离为第一种情况,故本题选C。
通过上述例题的讲解,相信考生对这一知识点有了更透彻的了解。
几何问题是历年数量关系考查的重难点,几何计算、几何特性、几何构造相结合考查,几何与其他题型如行程、概率等一起考查,需要考生有扎实的几何基础知识,灵活的应用才能让问题迎刃而解。更多相关考试信息请及时关注华图教育官网!