在行测考试中，工程问题是一类比较常见并且容易掌握的一个考点，工程问题中多者合作问题是大家比较感兴趣的一类问题，其难度系数不大只不过在运用过程中存在一些小问题，那今天华图教育就跟大家分享一下对于多者合作的常见题型以及解题技巧。
例题
一批货物，如果甲车单独运需要15天，如果乙车单独运需要10天，现在两车同时运，多少天能够运完这批货物?
A.6 B.7 C.8 D.10
【华图解析】已知题干中分别给出甲、乙单独完成同一项工程所需要的时间：15天和10天，大家看到这样的一道题，能够知道为工程问题，即工作总量=工作效率×工作时间。通常大家把工作总量特值为1，进而甲的效率可表示为
乙的效率可表示为
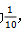甲乙同时运将二者效率进行加和，工作时间等于工作总量除以工作效率
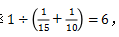选择A。但也会发现解题过程中有个问题就是对于分数加减法通分可能会出错，我们可以观察一下分数是怎么来的，总量除以时间得到的，而总量也是大家习惯性的设为1，那实际上总量都是特值而来的一个数据，不妨特值成方便计算的数据即时间的最小公倍数。
方法二：把工作总量表示为甲所需时间15的倍数，乙所需时间10的倍数，即可以表示为两者的最小公倍数30，
工作时间等于工作总量除以工作效率选择A。
多者合作问题中，常用的解题方式是特值法，我们可以将工作总量特值为1，也可以将工作总量特值为完成相同工作的若干个时间的最小公倍数。
例题
某市有甲、乙、丙三个工程队，工作效率比为3∶4∶5。甲队单独完成A工程需要25天，丙队单独完成B工程需要9天。若三个工程队合作，完成这两项工程需要多少天?
A.6 B.7 C.8 D.10
【华图解析】题干给出三个工程队工作效率之比,但是并不代表实际的数值，可以按照比例表示出三者的效率，不妨把甲的效率设为3x，乙的效率设为4x，丙的效率设为5x，已知甲的工作效率还给出了甲完成A工程需要的时间，可以得到A的工作总量即为
已知丙的工作效率和完成B工程所需要的时间可得到B工作总量即为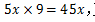
三队合作两项工程的时间等于两项工作量加和除以三队效率加和即为
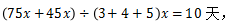选D。
实际上我们发现涉及到的未知数在求解过程中直接消掉了，对于结果并没有什么影响，故而多者合作中已知各部分效率之比或可推导出效率之比的时候，可以设效率为特值。
例题
A工程队的效率是B工程队的2倍，某工程交给两队共同完成需要6天，如果两队的工作效率均提高一倍，且B队中途休息一天，问：要保证工程按原来的时间完成，A队中途最多可以休息几天?
A.4 B.3 C.2 D.1
【华图解析】已知A的效率为B效率的二倍，故特值B的效率为1，A的效率为2，已知两个队共同完成某工程的时间，即某工程的工作量为
两队效率均提高一倍后B的效率为2，A的效率为4，按照原来的时间完成也就是6天，求A最多休息的天数，B休息的最少，题干中为1天，即B工作了5天完成的工作量为
个工作量由A完成，所需天数为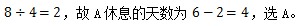
通过以上几个例题相信大家已经了解了工程问题的常见题型以及解题方法，希望对大家能有所帮助。
