首先,掌握原则是根本。很多考生对陌生的图形推理无从下手,这里以规律类的图形推理为例,图形推理总体性的做题原则无非就是同中求异,异中求同的过程。也就是说,如果图形中给出的图形在元素组成上各不相同,那要找到他们之间的规律,就必须找出他们图形中的相同点,聚焦共性;而如果图形组成元素相同,要找出他们之间的规律,就必须要找他们的不同点。以下图为例:
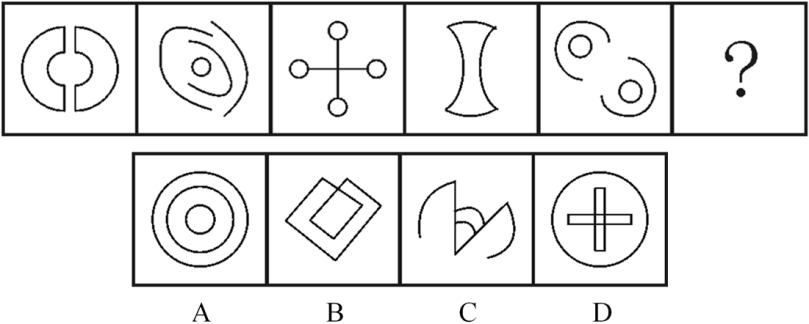
题目中给出的五个图形各不相同,那么要想找到他们的规律就得找出他们的相同点,即每个图形中都有曲线,那么曲线就是这几个图形的共性,据此可以排除B项,其他几项都有曲线,那么要想得到答案就得找出ACD的区别在哪里,通过观察,我们可以发现三个图曲线的数量不一致,根据曲线数量就可以选出答案C。
其次,观察特征是关键。每次授课都会发现有些考生在图形分模块讲解和做题时,正确率都比较高,然而在做综合练习题或者套题时极易出错。究其根本,还是对图形特征没有重视。根据图形的外形,每道题目中的图形无非呈现三种特性:相同、相似、完全不同。不同的图形特征对应着不同的做题方法。
第一,如果图形组成完全相同,只是局部元素的位置有变化,那么考虑它是一个位置类的规律,即平移、旋转或者翻转,当然也有可能是三种方式的结合。
第二,如果图形的组成元素有相同的地方,也有不同的地方,那么就考虑它是一个样式类规律的题目,即样式的遍历、运算。同时,如果将大的规律方向已经锁定在样式类的规律了,还要注意解题顺序,即先考虑样式遍历,再考虑样式的加减同异运算。
第三,若图形组成各不相同,即图形凌乱,那么要考虑两个方面的规律,因为我们知道数量类和属性类规律的图形特征都是图形不同,因此拿到图形不同的题目时,优先考虑属性类的规律,因为属性的规律较简单,只有对称、曲直和封闭性,如果没有这三种的特性,再去考虑数量类点、线、角、面、素的规律。而且数量类的这几个可数对象的数法是从宏观到微观去看,即:素、面、角、线、点的顺序。
例如下面这个题:
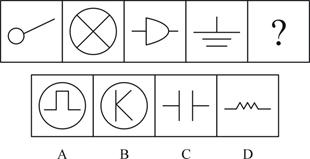
题干中图形各不相同,优先考虑数量或属性。同时异中求同,聚焦题干图形的共性是每个图形中都有直线,考虑直线的数量,题干图形的直线条数依次为1、2、3、4,呈等差数列,问号处图形应有5条直线,只有A项符合规律,因此选择A 选项。
综上,只有掌握了做图形题的整体原则,才能在见到陌生图形时从容不迫的整理好思路,提高做题的正确率。