我们先来看一个简单的例子,浓度为10%和20%的盐水混合,混合后其溶液浓度范围为10%-20%,一定位于两浓度之间。100g浓度为10%和100g浓度为20%的盐水混合,混合后其溶液浓度为15%,为两个混合溶液浓度的平均数,那么此时我们发现如果10%的溶液多于20%的溶液,那么他就会更稀一点,浓度介于10%-15%之间。反之,如果20%的溶液多与10%的溶液,那么他就会更浓一点,浓度介于15%-20%之间。这是我们十字交叉法在数量关系中的运用,同理,我们也可以把这个知识运用到资料分析中。
先来说几个常用的模型,上半年的增长率和下半年的增长率可以组成全年的增长率,进口额的增长率和出口额的增长率可以组成进出口总额的增长率,城镇收入的增长率和乡村收入的增长率可以组成城乡总收入的增长率……,这些模型都可以仿照浓度问题的十字交叉法思想去思考。我们下面来看几个例题。
例1 2018年上半年A企业实现净利润2607亿元;反映经营成长性的拨备前利润达到3807亿元,同比增长8.9%。净利润和拨备前利润增速均为近年来同期最高。根据财报数据,2018年一季度净利润1321亿元,增速为15.7%,二季度净利润增速较一季度明显放缓,二季度净利润增速仅为6.6%。问题:2018年上半年A企业净利润增速为:
A.1.1% B.3.5% C.10.2% D.15.9%
【解析】由材料可知,2018年一季度A企业净利润增速为15.7%,二季度净利润增速仅为6.6%,结合十字交叉法可知,2018年上半年A企业净利润增速应介于6.6%~15.7%之间,只有C符合。
例2 2017年,A省完成邮电业务总量6065.71亿元。其中,电信业务总量3575.86亿元,同比增长75.8%;邮政业务总量2489.85亿元,增长32.0%。问题:2017年A省完成邮电业务总量同比增速在以下哪个范围之内?
A.低于25% B.25%~50%之间 C.50%~75%之间 D.超过75%
【解析】2017年A省电信业务总量3575.86亿元,同比增长75.8%;邮政业务总量2489.85亿元,增长32%。由十字交叉思想可知,2017年邮电业务总量同比增长率介于32%~75.8%之间,排除A项;简单比较可知,2016年电信业务总量高于邮政业务总量,故2017邮电业务总量同比增长率介于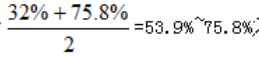 之间,排除B项;因为2016年电信业务总量与邮政业务总量相差不大,故2017年邮电业务总量同比增长率更靠近53.9%,不会超过75%,选择C项。
之间,排除B项;因为2016年电信业务总量与邮政业务总量相差不大,故2017年邮电业务总量同比增长率更靠近53.9%,不会超过75%,选择C项。
以上两个题从易到难,例1主要是让我们理解混合之后的增长率一定介于混合前两者增长率之间,例2则是让我们理解混合后增长率大小还和两部分的实际值有关,谁大,总的增长率就更靠近与谁。










