随着市考公告的发布，相信很多小伙伴已经开始了紧张地备考，近几年公考竞争越来越激烈，进面分数也越来越高，对于备考的小伙伴来说，压力越来越大。在考试科目中《行测》的难度最大的，大家也会投入大量的时间来复习，《行测》科目包括常识判断、言语理解与表达、判断推理、数量关系、资料分析五个部分，其中的数量关系是大家非常畏惧的一部分，很多小伙伴甚至放弃了这一部分，从近几年的进面分数来看，这样的做法是非常不可取的。要是放弃其中某一个部分，进面的机会会大大降低。

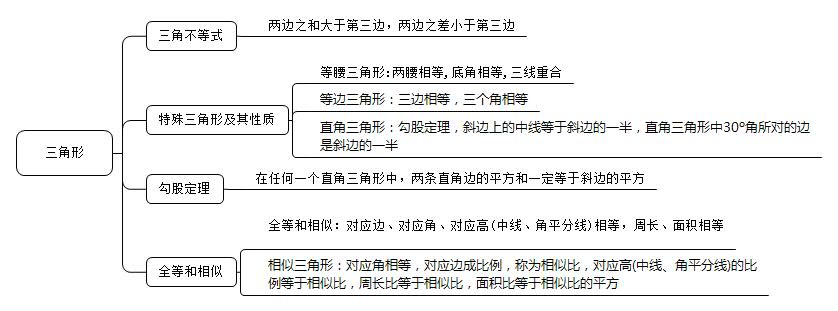
　　从近几年的联考真题来看，在数量关系这一部分中几何问题可以说是一个必考题型，并且所占的比例也越来越高，而三角形又是几何图形中考的最为频繁的一个。那么我们就来整理一下三角形的知识点：

　　(1)三角不等式

　　三角形三边之间具有如下关系：两边之和大于第三边，两边之差小于第三边。

　　(2)特殊三角形及其性质

	图例	性质
等腰三角形		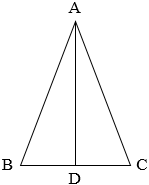两腰相等：AB=AC	底角相等：	三线重合：顶角平分线、底边上的中线、底边	上的高线，三线重合
等边三角形		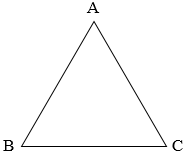三边相等：AB=BC=CA	三个角相等：
直角三角形		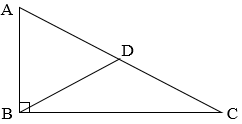勾股定理：		斜边上的中线等于斜边的一半：		直角三角形中30º角所对的边是斜边的一半。

　　(3)勾股定理

　　勾股定理：在任何一个直角三角形中，两条直角边的平方和一定等于斜边的平方。常用勾股数(3、4、5)，(6、8、10)。

　　(4)全等和相似

	判定	性质
全等三角形	①两边及夹角对应相等	②两角及夹边对应相等	③三边对应相等	①对应边、对应角、对应高(中线、角平分线)相等	②周长、面积相等
相似三角形	①两角相等	②两边对应成比例且夹角相等	③三边对应成比例	①对应角相等	②对应边成比例，称为相似比	③对应高(中线、角平分线)的比例等于相似比	④周长比等于相似比，面积比等于相似比的平方

　　三角形是最基础的平面几何图形，在几何题目中平行四边形、矩形、梯形等多边形也是常见的图形，但是这些图形都可以视为由三角形组成的。常见的题目中直接公式计算、性质运用、等底同高构造等都是常见的解题方法。

　　我们来练习一道真题：

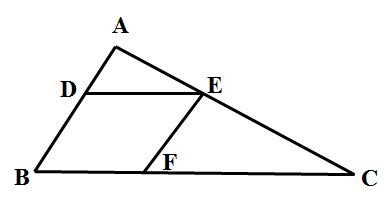
　　【例】一块三角形农田ABC(如下图所示)被DE、EF两条道路分为三块。已知BD=2AD，CE=2AE，CF=2BF，则三角形ADE、三角形CEF和四边形BDEF的面积之比为：()

　　A.1:3:3

　　B.1:3:4

　　C.1:4:4

　　D.1:4:5

　　本题考查的是几何问题，利用三角形的相似性质，相似三角形对应的边成比例，周长比等于相似比，面积比等于相似比的平方来解题。由BD=2AD，CE=2AE，CF=2BF可知，四边形BDEF为平行四边形，则，则△ADE与△EFC与△ABC相似，相似比的平方等于面积比，所以S△ADE：S△CEF=1:4，S△ADE:S△ABC=1：9，设S△ADE面积为1，S△CEF的面积为4，S△ABC的面积为9，则四边形BDEF的面积为9-1-4=4，因此，三角形ADE与四边形BDEF的面积比为1：4，所以三者比值为1:4:4。答案选择C选项。