有些分步类排列组合概率问题看似复杂,若直接采用概率法去解题将会省去很多步骤,从很大程度上减少计算难度,大大提高解题效率。下面华图老师会将这类题型的套路以及解题技巧进行归纳总结,帮助大家在考试中顺利得分。
【例1】某学校举行迎新篝火晚会,100名新生随机围坐在篝火四周。其中,小张与小李是同桌,他俩坐在一起的概率为:
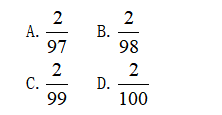
【答案】C
【解析】
解法一:环形排列+捆绑法

当然,有部分同学不能够熟练掌握环形排列和捆绑法的技巧,可直接使用概率法去解题,具体操作方法如下:
解法二:概率法
第一步,本题考查基本概率,用分步概率法解题。
第二步,100名新生随机围坐在篝火四周,即会产生100个座位,假定小张选择任一个位置坐下,则小李只能从剩余的99个位置中选择坐下,与小张坐在一起的情况有两种,即坐小张的左右两侧。

因此,选择C选项。
从解法二中我们能够直观地感受到概率法的简单明了之处,不仅列式简单,计算量也小,并且易于理解,推荐考试时直接使用。
【例2】某次圆桌会议共设8个座位,有4个部门参加,每个部门2人,排座位时,要求同一部门的两人相邻,若小李和小王代表不同部门参加会议,则他们座位相邻的概率是:
A.1/48 B.1/24
C.1/12 D.1/6
【答案】D
【解析】
解法一:环形排列+捆绑法
第一步,本题考查概率问题。

因此,选择D选项。
解法二:概率法
第一步,本题考查概率问题。

【例3】某单位工会组织桥牌比赛,共有8人报名,随机组成4队,每队2人。那么小王和小李恰好被分在同一队的概率是:
A.1/7 B.1/14
C.1/21 D.1/28
【答案】A
【解析】
解法一:平均分组
第一步,本题考查概率问题。

这类题型共性解题思路:先选出其中一人确定概率为1,再根据题目要求计算另外一人和第一人相邻或者同一组的概率,最后进行分步概率的相乘,计算出结果。此类题目,长相类似,容易识别,多进行强化练习,考试遇到此类题型,可以按照这个套路得分。










