-->

　　图形推理一直是公务员考试的难点之一，很多时候我们比较难第一时间去找到合适的规律，因为同学们学完相关图形推理的理论知识后，往往脑海中有许多的解题方法，往往会不知道优先选择那种方法来首先去用，这种时候往往就需要我们多去总结各种所学的图形推理规律的应用条件，今天就来一起看下图形推理章节关于数量类点的数量的规律应用。

　　关于的点的个数规律往往其实不算非常复杂，往往常见的是递增、周期、常数规律等，但是在解题时什么时候去寻找点的个数之间的规律呢，如果我们没有优先去查点的个数而是查了角或是面的个数发现行不通之后再来查点，这往往就比较耗费我们的时间。根据我们过往做题的经验总结发现：往往当发现图形并不是封闭图形时或者图形里有非常明显的线条相交时，再或者是图形中有比较特殊的点比如切点这类特殊点时，当出现以上情况时，我们往往优先考虑应用点的数量规律，我们具体来通过例题来分析下：

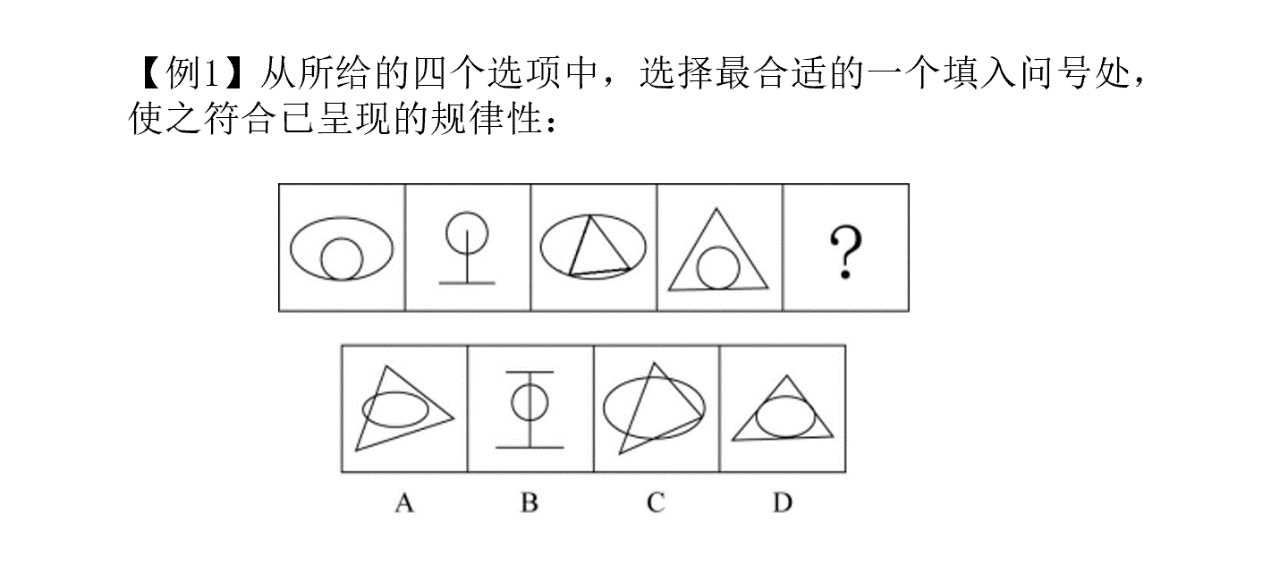
　　我们拿到一道题后，第一步观察特征，发现题干所给各个图形的组成元素不同，这时优先去考虑图形的数量或属性规律，但是呢我们能够看到第一幅图相切特征非常明显，这时我们会想到优先考虑点的数量，再者第二幅图并不是一个封闭图形，这时我们可以判定优先去寻找点的数量规律，查完所有图形的点个数后，我们便能够很快的找到题中点的个数是属于递增的规律，从而快速得出答案A。通过在拿到题目后进行对题干的分析结合我们具体应用点的数量规律的条件，可以很快速的判定这道题目应该是优先选择点的数量规律进行解题，从而避免在解题过程中频繁的尝试各种规律而浪费时间。那我们再来看一道题目：

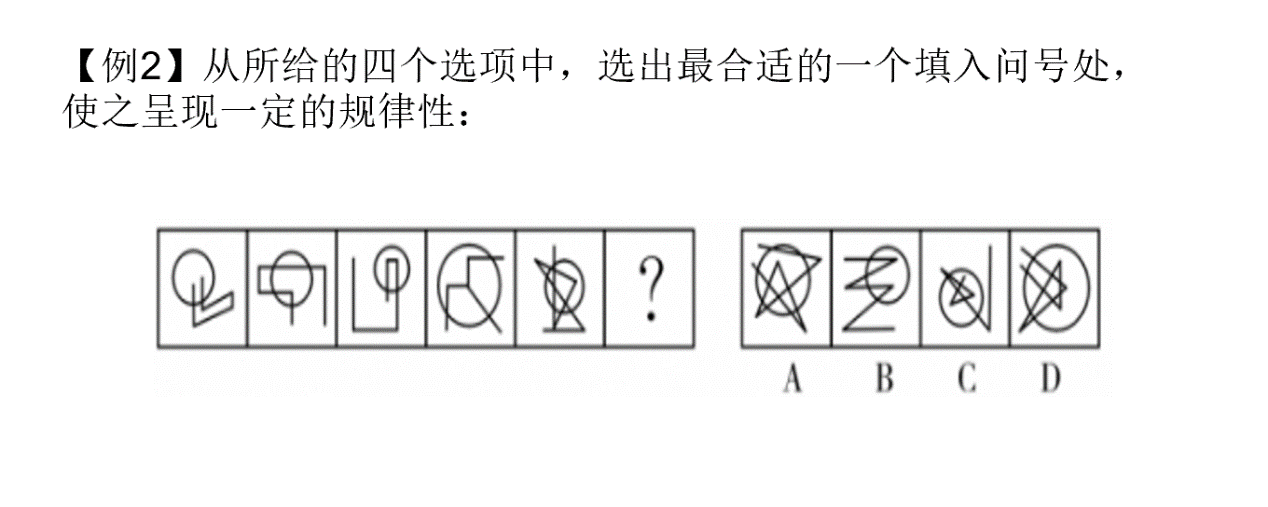
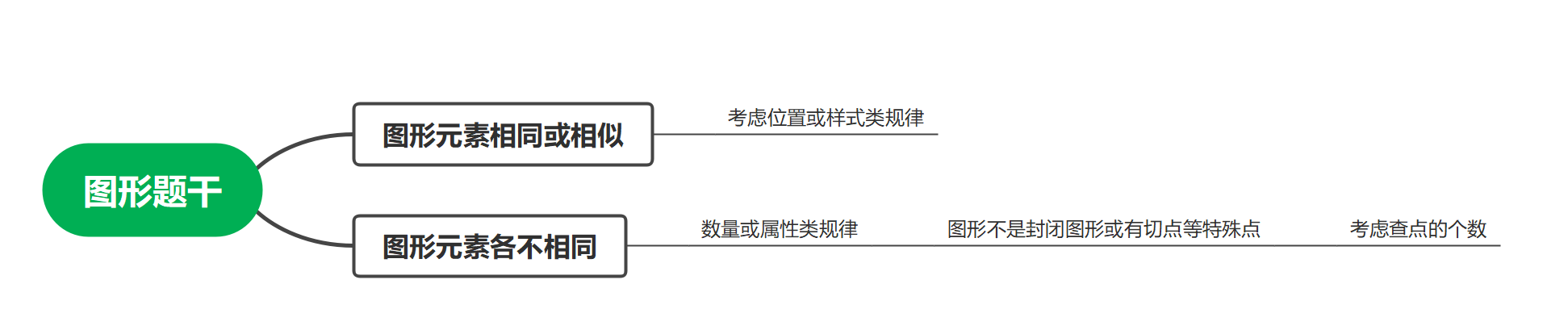
　　看到题目后，第一步仍是观察整体图形特征，能够发现图中各个组成元素不同，仍优先考虑数量或属性类规律，观察发现题干中所给出的图形都不是封闭图形，这时可以优先考虑去查点的个数，这时我们又会发现题目中图形既有交点，还有端点，那我们把这两类点的个数数完发现并没没有找到规律，这时我们能发现每个图都有圆形，虽然整幅图不是封闭图形，但是图中的圆形是封闭图形，这时能够去想圆内的点或是圆外的点，这样就能够选出最终答案C。其实，现在无论是国考还是公务员考试都很少直接考察点的个数了，更多的情况都是会对点进行限定，要么是点的类型限定，比如交点、切点、端点或是Y型点、T型点等等，另外也会对点的位置进行限定，比如封闭图形内部的点或外部的点，这时我们要看原图去寻找各个图形的共同之处，同时也要在平时做题时多去总结这些相关的规律，这样能够在真正考场做题时更加有意识的向多方面来考虑，最后我们来用思维导图的形式进行下总结。