在数字推理中,对于没有明显特征的数列,大多为多级数列。多级数列进行运算的时候,优先考虑做差,再考虑做和,最后做积。多级数列经过做差、和、积、商之后,得到的子数列都是简单的基础数列。首先对数列进行观察,数列变化较为平缓就进行一次做差,再两次做差,得到基础数列。但是最多做到两次差,如果不行就要考虑改变方法。下面我们看看“做差法”在实际题目中的运用。
【例】-5,-3,4,16,33,( )
A. 55 B. 56
C. 57 D. 58
【答案】A
【解题技巧】数列没有明显特征,且变化趋势平缓,优先考虑做差。做一次差如图所示:
一次差数列为公差为5的等差数列,差数列下一项为22,则未知项为33+22=55。
因此,选择A选项。
【例】1,3,6,11,18,( )
A. 25 B. 27
C. 29 D. 33
【答案】C
【解题技巧】数列没有明显特征,且变化趋势平缓,优先考虑做差。做一次差如图所示:
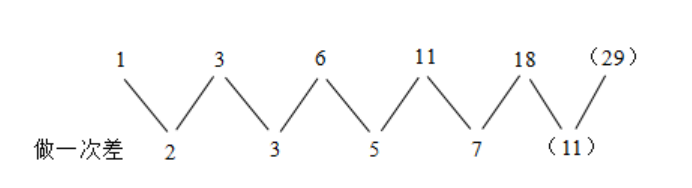
差数列是连续质数数列,7后面的质数为11。则所求项为18+11=29。
因此,选择C选项。
【例】5,12,21,34,53,80,( )
A. 121 B. 115
C. 119 D. 117
【答案】D
【解题技巧】数列没有明显特征,且变化趋势平缓,优先考虑做差。做两次差如图所示:
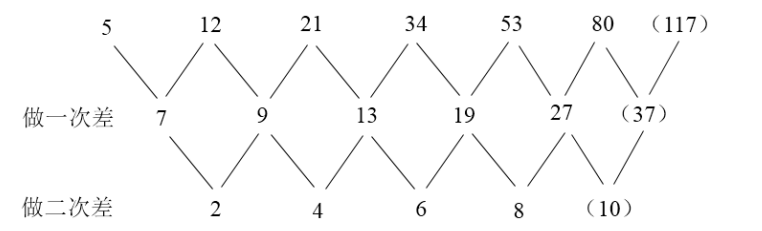
二次差数列是公差为2的等差数列,则下一项为8+2=10,一次差数列下一项为27+10=37,所求项为80+37=117。
因此,选择D选项










