多次相遇问题在考试当中作为事业单位的常见考点,时常令部分考生望而生畏,但只要把其中规律理清楚,多次相遇问题其实很容易解答,下面通过最普遍的“异地相遇问题”进行梳理说明。
甲乙两车同时从A、B两地以均匀的速度出发相向而行,在第一次相遇后继续向前,达到对方起点后立即返回,在第二次相遇后继续向前,当回到起点后又立即返回,如此往复运动一直到第n次相遇。下面通过前三次的相遇情况分析甲乙两车的行进特点。
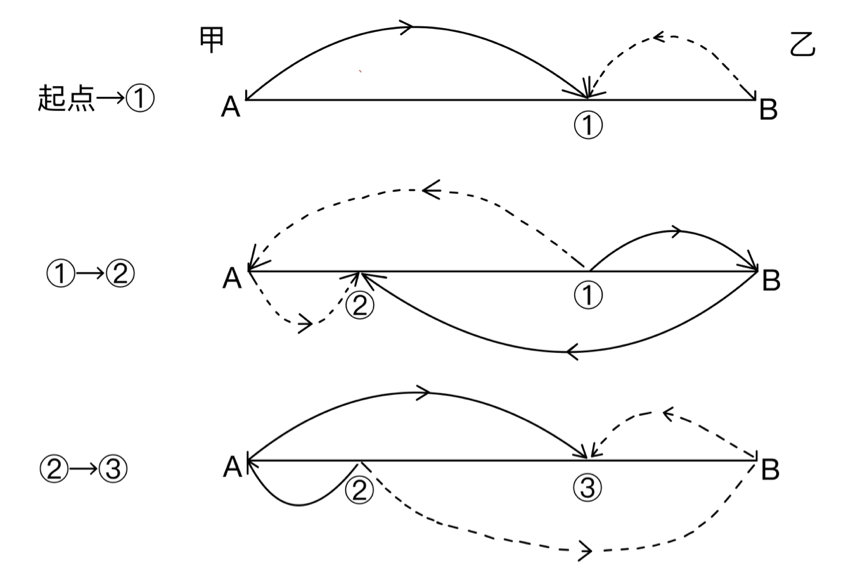
如上图所示,在行程图中分别通过实线和虚线表示甲乙两车的行驶路径。从开始到第①次相遇,甲乙共行驶了一个AB的全程为S;从第①次相遇到第②次相遇,甲乙共行驶了两个AB的全程为2S;在第②次到第③次相遇,甲乙同样行驶了2S;由此推出在往后每一次相遇与下一次相遇两人所走的路程均为2S。
接下来重点分析从开始到第②次相遇的情况,甲乙一共走了三个AB的全程为3S,因为相遇时路程和=速度和×时间,既S=(V甲+V乙)× t,由于甲乙速度保持不变,当路程和为3S时,时间为3t。而对于甲乙独自行驶的路程而言,从开始到第①次行驶的路程为:S甲(乙)=V甲(乙)× t,当时间为3t时,路程为3S甲(乙),即从开始到第②次相遇时甲或乙走的路程,是从开始到第①次相遇所行驶路程的3倍。由此往后推出从开始到每一次相遇的情况,规律总结如下:
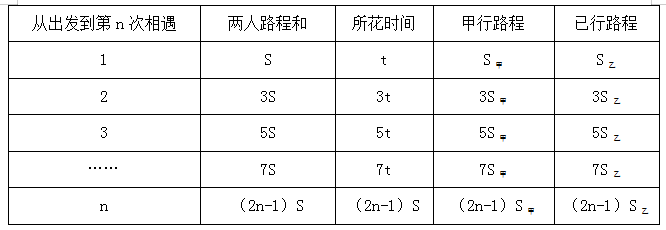
而在实际考试当中,最常运用到的是从开始到第②次相遇时,甲或乙走的路程,是从开始到第①次相遇所行驶路程的三倍。注意熟练运用此项规律,将帮助我们巧妙解答“多次相遇问题”,下面通过两道题进一步加深理解运用:
1.甲、乙两人以均匀的速度分别从A、B两地同时出发,相向而行,他们第一次相遇离A地7千米,达到对方出发点后立即返回,第二次离B地5千米,则A、B两地相距多少千米?
A.13 B.16 C.17 D.21
答案:B
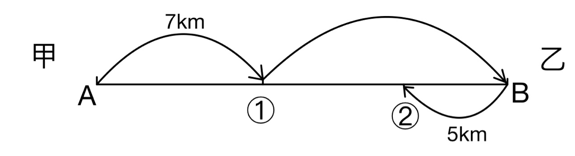
解析:如图所示,对甲而言,从出发到第②次相遇所走的路程是从出发到第①次所走路程的3倍,第一次相遇时甲走了7公里,第二次相遇时甲共走了7×3=21公里,AB两地相距为21-5=16公里。故本题选B。
2.甲、乙两汽车分别从P、Q两地同时出发相向而行,途中各自速度保持不变。他们第一次相遇在距P点16千米处,然后各自前行,分别到达Q、P两地后 立即折返,第二次相遇在距P点32千米处,则甲、乙速度之比为:
A.1:2 B.2 :3 C.2:5 D.3:4
答案:B
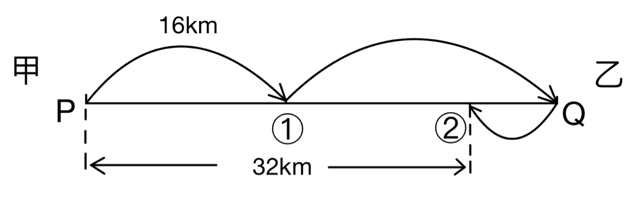
解析:速度=路程÷时间,要求速度比,应求相同时间内甲、乙经过的路程比。从开始到第②次相遇,甲一共走了16x3=48千米,则全程为(48+ 32)÷2= 40千米,第一次相遇乙走了40﹣16= 24千米,则甲、乙速度之比为16:24= 2:3,故本题选B。










