事业单位备考,数量关系部分一直是大多数考生觉得比较难的部分,但是也有很多有效的方法可以帮助我们。针对极值问题这种比较常见的题型,接下来,就给大家分享解决这类题的一种方法—均值不等式。
一、均值不等式是啥

二、均值不等式咋用
1、和定差小积大
例:已知a+b=10,求ab的最大值?
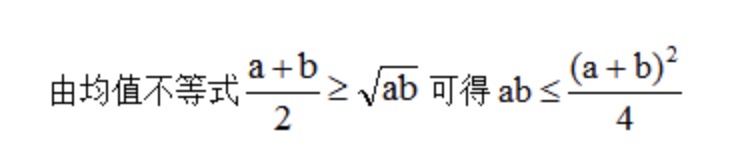
故当a+b为定值时,ab有最大值,当且仅当a=b时等号成立,即当a=b=5时,乘积ab取到最大值,最大值为5×5=25。
总结规律:两个数的加和为定值时,两数之间的差值越小,两个数的乘积越大。
2、积定差小和小
例:已知ab=16,求a+b的最小值?
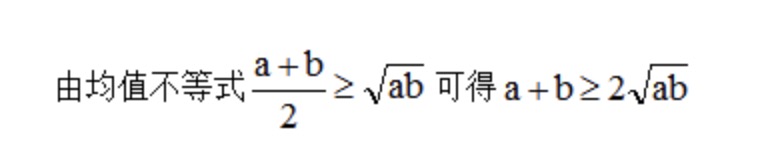
故当ab为定值时,a+b有最小值,当且仅当a=b时等号成立,即当a=b=4时,a+b取到最小值,最小值为4+4=8。
总结规律:两个数的乘积为定值时,两数之间的差值越小,两个数的加和越小。
三、例题精讲
【例题1】已知长方形的周长为16厘米,求长方形的面积最大是多少平方厘米?
A.15 B.16 C.17 D.18
【答案】B
【解析】设长方形的长为a,宽为b,由周长为16厘米可得2(a+b)=16,即a+b=8,由均值不等式可得,当且仅当a=b=4厘米时,乘积ab即长方形的面积取到最大值,所以最大值为4×4=16平方厘米,故选B。
【例题2】将进货单价为90元的某商品按100元一个出售时,能卖出500个,已知这种商品如果在原售价的基础上每个涨价1元,其销售量就会减少10个,为了获得最大利润,售价应定为( )
A.110元 B.120元 C.130元 D.150元
【答案】B【解析】设售价上涨了x元,即售价为(100+x)元,销量为(500-10x)个,设总利润为y,则由题意得,y=(100+x-90)(500-10x)=(10+x)(500-10x)=10(10+x)(50-x),由于10+x+50-x=60,是一个定值,所以根据均值不等式,当且仅当10+x=50-x时,y有最大值,即x=20时,能获得最大利润,此时售价为100+20=120元,故选B。根据以上两道例题重点要了解均值不等式如何使用,记住解题思路和方法,后期还有多多刷题练习,熟练掌握。










