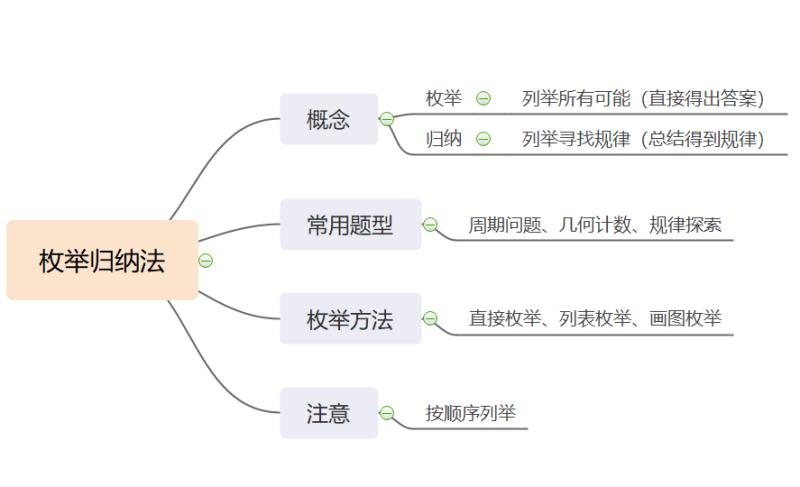
知道了枚举归纳是什么后,就要考虑什么时候可以用。比如说题目当中有一些周期类的推算,比如说我们几个人轮流做一件事情,隔几天谁出现一次,隔几天谁再来一次这种周期类的,我正常求解这个周期不好找或者是不好解,可以通过枚举的方式列举;还有一些几何计数类的,比如说给我一些图形,这里面有一些特殊的形状或者特殊的颜色让我去标记它大概出现几个;还有一些规律探索类的,比如说我们的题目当中明显会出现一些市略号,或者以此类推这样的文字表述,那我们没有特别好的办法的时候,都可以尝试用枚举归纳的方式去找一找答案。
那我们来看一下题目具体是怎么用的,接下来我们来看一道题
【例 1】(2019 联考)小王在商店消费了 90 元,口袋里只有 1 张 50 元、4 张 20 元、8 张 10 元的钞票,他共有几种付款方式?
A、5
B、6
C、7
D、8
可以使店家不用找零钱?我们在读题的时候会发现,其实这个题的表述非常简单,我就想凑90块钱,然后让他不用找零,那就是拿我现有的零钱去凑成90,我们再观察一下选项,会发现选项的数据也不大,我要是让你在这个题当中直接列出一个式子,找到一个公式很困难,选项数据不大,如果我们没有更好的办法,那就可以把所有的情况全都列举出来,就是拿我口袋里的钱去凑90就可以了,那怎么去凑呢?你看我们有50元的,有20元的,还有10元的,建议大家先从大的开始用,再不停的再去往下调换,比如说我就以50的为主,我最开始在这个凑这个钱的过程当中呢,先以50的为准,那我只有一张50的凑不出我们想要的90元对不对,那50的不行咱们再接着往后凑,我是从大面额开始找的呀,那我就开始继续用大面额的,那这样的替换过程中我就可以
50元 20元 10元
1张 2张
1张 1张 2张
1张 0张 4张
0张 4张 1张
0张 3张 3张
0张 2张 5张
0张 1张 7张
那我再换的话,我把20也去掉全用10行不行?大家会发现10元的钞票,它总共只有8张,不可能凑出90元,所以说我们列举的情况就只能有7种了,那答案选择的是C。我们总结一下这个题,第一我们是在去运算的过程当中呢,发现找不到合适的式子,但是能读懂题目,而且选项的数据不大,我们最终确定可以通过枚举的方式进行求解;第二为了避免不重复不遗漏,我们按一定的顺序去枚举,这题我们用的是从大到小,后面同学们也可以选择从小到大,无论哪一种,结果都不会出现重复,这也就是我们所说的有序枚举。
最后,我们来总结一下吧,请看下图