最值问题一直是上考行测备考过程中非常重要的题型，它包含了最不利构造，数列构造和多集合反向构造这三种题型，因为最值问题的题目难度适中，解题方法相对固定，因此在备考过程中，这类题型是大家在行测数学运算学习过程中非常重要的得分项。在过去的2021年上考中，最值问题里的数列构造问题均有所体现，数列构造从解题方法上看相对比较固定，逻辑很清晰，但是其中又有很多陷阱和注意事项，如果不经过系统的梳理复习，很可能当我们遇到数列构造问题时，仍然不能很好的解决问题。因此我们本期就围绕最值问题中的数列构造问题进行解答，帮助大家攻破数列构造的难关。

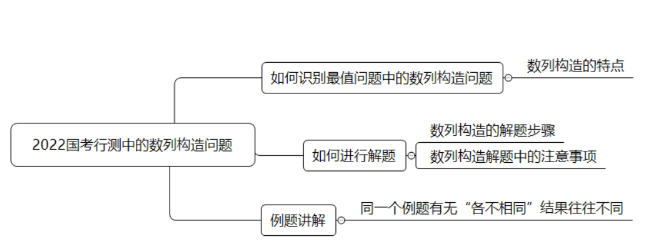
1、如何识别最值问题中的数列构造问题?

首先，这类题目属于最值问题的范畴，提问方式会涉及到包含“最”、“至”这类的表示极限的词，如果我们看到题目的提问里面包含“最………最”这样的表述，或者“排第几……至”这样的表达时，这样我们就可以判定该类题型为数列构造问题。

2、如何进行解题?

第一步：对数列按照从大到小或者从小到大的顺序进行排序;

第二步：定位所求数据为X;

第三步：按照题目的要求进行构造;

第四步：将构造出的数列相加求和，解得X的值即可。

在解题的过程中，第三步要注意题目中是否含有“各不相同”几个字，第四步注意如果求得的X为非整数时，要就行取整，我们的口诀是“问最小取大值，问最大取小值”。

3、例题讲解

【例1】从某物流园区开出6辆货车，这6辆货车的平均装货量为62吨，已知每辆货车载重量各不相同且均为整数，最重的装载了71吨，最轻的装载了54吨。问这6辆货车中装货第三重的卡车至少装载了多少吨?

A. 59

B. 60

C. 61

D. 62

【答案】B

【解析】根据设问方式为第三重的……至少……判定为数列构造，然后对数列进行排序，总共6辆车，按照从大到小的顺序，假设排第三重的至少装载了x吨，且每辆货车载重各不相同，

1 2 3 4 5 6

71 70 x x-1 x-2 54

最后6辆车加和为：71+70+x+x-1+x-2+54=62×6，解得x=60。

因此选择B。

此题如果题干中没有“各不相同”这几个字，则数列构造的情形就不相同，我们就例题1进行变形：仍然按照从大到小进行构造为：

1 2 3 4 5 6

71 70 x x x 54

进行加和为71+70+x+x+x+54=62×6，解得x=59。

因此选择A。

综合上述两种情况，同一个例题，如果题干中没有数列每项各不相同，则构造就不一样，需要认真分析，然后仔细求解，只有这样才能将数列构造真正的弄清楚。