工程问题在行测数量关系的题目中经常出现，并且相对来说是比较简单的，只要我们掌握了一定方法会发现这一类题目其实还是值得一做的。因此华图教育通过几个例题来告诉大家，工程问题到底怎么来解决。
例1
一项工程，甲单独做要10天，乙单独做要15天。若甲、乙两人合作，需要多少天?
A.5 B.6 C.7 D.8
华图解析：这道题中，我们会发现题目中出现了甲完成此项工程的时间，也出现的乙完成此项工程的时间，那我们想要求出合作的时间就需要知道此项工程的工作量和甲、乙的工作效率，所以这里不妨我们设总工作量为“1”。则甲
天。所以这道题选B。
这道题在计算时其实是有分数计算的，有没有什么方法可以再简单一点呢?其实无论设工作总量为多少都不会影响最终的结果，为了计算简便，就要让效率为整数。如果效率为整数就要让工作总量为时间的倍数，所以也可以设时间的最小公倍数为工作总量。设工程总量为10、15的最小公倍数30，则甲的工作效率为3，乙的工作效率为2，则甲、乙两人的合作效率为
故甲、乙两人合作需要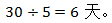
故本题选B。
总结：题目中出现完成同一项工程的多个时间时，可以设时间的最小公倍数为工作总量。
例2
甲、乙两队完成一项工程的效率比为2∶5。该项工程，若由甲队先单独做3天，再由乙队单独做4天，最后由甲、乙两队合作6天刚好完成。问若由甲队单独完成，需要多少天?
A.32 B.33 C.34 D.35
华图解析：这道题中想要求出甲单独完成要多久就需要知道整个工程的工作量，还有甲的工作效率。题目中出现了甲乙的效率之比，不妨结合比例设他们的效率分别为2x、5x，那整个工程的工作量就为
而这里我们发现其实到最后我们所设的x约掉了，所以直接设工作效率之比为工作效率就好了，因此不妨设甲、乙两队的工作效率分别为2、5，则工作总量为
故本题选C。
总结：题目中出现了工作效率之比，按最简比设工作效率。
经过上面几个题目的解析，大家可以发现，只要掌握了方法，工程问题也可以很简单。
